Lesson 8: Springs, pipes, vessels
In this lesson, we’ll delve into the fascinating world of springs, explore how they work, and discuss various types of springs. Additionally, we’ll learn about the pressure exerted by fluids on the walls of vessels and understand the principles behind dimensioning cylindrical tubes and vessels subjected to internal pressure.
- Springs
1.1 Characteristics of Springs
- Springs store mechanical work as deformation energy and convert it back into mechanical work.
- Their linear relationship between deformation and force makes them suitable for force measurement.
- Material choice and sizing depend on the expected stresses and load conditions.
- Fatigue limit consideration is essential for springs subjected to frequent alternating loads.
1.2 Relationships Characterizing Springs
- Relationship between deformation and loading force: f = f(F)
- Relationship between loading force and stress: 𝜎 = 𝜎 (F)
- Relationship between deformation and stress: f = f(𝜎)
- Amount of stored deformation work indicates the spring’s utilization.
1.3 Types of Springs
- Springs exhibit diverse functions, shapes, and behaviors.
- Types based on deformation include contracted/tensioned springs, torsion springs, and bent springs.
1.4 Specific Types of Springs
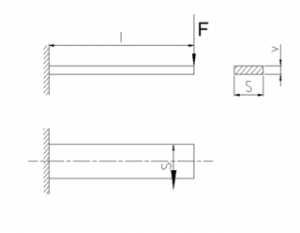
- Leaf Spring: A cantilever with a rectangular cross-section can be dimensioned using known relationships.
- The straight leaf spring is bent type, and can be dimensioned using the relationships already described.
- The inspected spring is a cantilever with a rectangular cross-section of dimension s x v.
- The relationship between deformation and force.

- Torsion Spring: A straight, cylindrical rod’s end is twisted by a moment
Mt = F∙p moment

- Helical Coil Spring: Most commonly used spring type, loaded by tension or compression at its ends in the direction of the cylinder axis. In the case of a tensioned spring, the threads move away from each other and the pitch increases), in the case of a compressed spring, the threads move closer together and the pitch decreases).


- Pipes, Vessels
2.1 Fluid Pressure on the Wall of an Arbitrary Shape Vessel
- Neglecting the weight of the fluid, the pressure p of a fluid is constant and perpendicular to the vessel wall.
- Thus, the projection of the resultant R of the pressures acting on the surface of AB curve in a given direction is equal to the pressure of the fluid on the projection of the surface AB perpendicular to that direction.
- Applies to liquids, vapors, or gases.
2.2 Dimensioning Thin-Walled Cylindrical Tubes and Vessels Under Internal Pressure
- Examining a thin-walled cylindrical vessel subjected to internal pressure:
- D = 2r: Inner diameter [mm]
- v: Wall thickness [mm]
- p: Internal pressure [N/mm²]
- Focus on the effect of internal pressure p, neglecting the weight of the medium.
- The Boiler Formula is derived for calculating tangential stress in the vessel wall.
2.3 Thin-Walled Sphere Under Internal Pressure
- A thin-walled sphere under internal pressure experiences principal stresses.
- The resultant force on a diametral plane is equal to the internal pressure.
2.4 Pipes Under External Pressure
- Pipes and vessels react differently under external pressure than under internal pressure.
- External pressure can lead to buckling, and it is typically applied to cylindrical pipes.
Understanding the principles behind springs and the effects of internal and external pressure on vessels and pipes is essential for engineers working with materials that need to withstand mechanical forces and fluid pressures. These principles are fundamental in various engineering applications, ensuring the safe and efficient use of these components in diverse industries.