Lesson 5: Stress states
In this lesson, we will delve into the concept of stress states, understanding how they are represented and visualized in engineering and mechanics.
- Spatial Stress State
- In the field of engineering and mechanics, representing stress states accurately is crucial. There are several methods to achieve this:
1.1 Elementary Unit Cube
- Imagine an infinitesimally small cube. This cube is employed to depict the stresses acting on three mutually perpendicular planes.
1.2 Stress Tensor
- The stress tensor is a mathematical representation used to describe the distribution of stresses within a material or structure. It provides a comprehensive view of stress components at every point within a body.
- As described earlier, the stress tensor represents stresses like so:
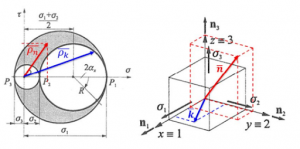
1.3 Mohr’s Circle
- Mohr’s Circle is a graphical method used to visualize relationships between normal and shear stresses on inclined planes within a stressed body. This tool can also calculate principal stresses, maximum shear stresses, and stresses on inclined planes. It is named after its creator, German Civil Engineer Otto Mohr (1835-1918).
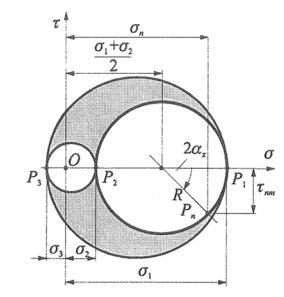
- The stress vectors for different directions in a σ-𝜏 coordinate system fall within two arc triangles. At points where 𝜏 (shear stress) equals 0, these directions correspond to the principal directions, which are mutually perpendicular.
Definition
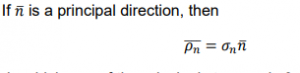
- Principal Plane: A plane where one of the principal stresses is equal to 0.
- Endpoints of Stress Vectors: These correspond to the directions of principal planes and are located on those planes.
- Drawing Mohr Circle: Mohr’s Circle is commonly drawn when at least one principal direction is known.
- Planar Stress State
In certain scenarios, the stress state simplifies to a planar state. This occurs when there is only one normal stress and one shear stress (a pair) in the stress tensor, and both are confined to a single plane. Key aspects of planar stress states include:
- In a planar stress state, one of the principal stresses is always zero.
- The spatial elementary unit cube can be reduced to a simplified, planar version.
Understanding stress states is fundamental in engineering and mechanics, as it allows engineers and analysts to assess how materials and structures respond to various forces and loads. Whether in three-dimensional spatial stress or simplified planar stress states, this knowledge forms the basis for making informed design and analysis decisions.
With this understanding, you are better equipped to analyze and design structures, ensuring they can withstand the stresses and loads they encounter in real-world applications.