Lesson 1: Center of gravity – centroid
In this lesson, we’ll delve into the concept of the center of gravity and centroid, exploring how to calculate their positions for various objects and shapes.
- Introduction to Center of Gravity and Centroid
- Gravity affects every object on Earth, creating a spatially distributed force system.
- For simplification, this force system can be replaced by its resultant, with the acting point known as the center of mass.
- In geometry, the center of mass of an object with uniform density is referred to as the centroid.
1.1. Calculating the Centroid Location
- Each coordinate of the centroid’s location vector can be computed as the sum of the product of the volume and the coordinate of each part, divided by the total volume.
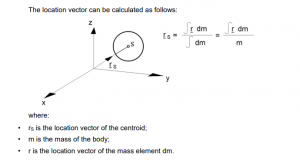
Calculating the Centroid Location
1.2. Centroid of Planar Shapes
- Planar shapes primarily deal with surface area.
- The centroid’s coordinates can be determined by summing the product of the area and coordinate of each part, divided by the total area.
- Knowledge of centroid coordinates for basic planar shapes is essential.
1.2.1. Centroid of Basic Planar Shapes
- Understanding the centroid positions for fundamental planar shapes.
1.2.2. Centroid of Composite Planar Shapes
- Composite planar shapes can be analyzed by dividing them into basic parts.
1.3. Centroid of Lines
- For lines, the significant dimension is length.
- Each coordinate of the centroid’s location vector can be found by summing the product of the length and coordinate of each part, divided by the total length.
- Knowledge of centroid coordinates for basic lines is crucial.
1.3.1. Centroid of Basic Lines
- Exploring centroid positions for fundamental line segments.
1.3.2. Centroid of Composite Lines
- Complex lines can be analyzed by breaking them into basic segments.
1.3.3. Practical Examples of Line Centroid Calculations
- Real-world applications of line centroid calculations:
- Cutter: Calculating the point of action for a stamp cutter to precisely position a hydraulic piston, avoiding bending loads.
- Trusses: Simplifying the calculation of center of mass for prismatic components within trusses.
- Substitution: Streamlining centroid calculations for complex structures by substituting segments with weighted lines, employing the superposition principle.
- Human Body: Demonstrating how even the human body can be analyzed by segmenting it at joints, enabling the calculation of the center of mass in various body positions.
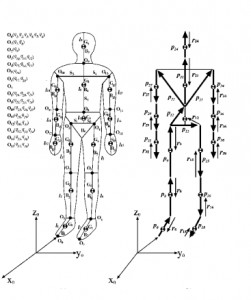
Conclusion:
- Understanding the center of gravity and centroid is essential for engineering and design, as it enables the precise analysis of how forces and weight are distributed in objects and structures.
- The centroid simplifies complex calculations by providing a single point of reference for geometric shapes, whether they are planar or linear.
- Practical applications, such as determining the point of action in cutting processes, optimizing truss designs, and simplifying complex structures, showcase the real-world significance of centroid calculations.
- By grasping these concepts, engineers and designers can create more balanced and efficient solutions for a wide range of applications, from architecture and machinery to aerospace and beyond.
- The knowledge of centroid calculation extends to even analyzing the human body’s center of mass, highlighting the versatility and universality of this fundamental concept in various fields of study and application.