Lesson 8 – Kinetics of particles and rigid bodies
2.4. Kinetics of particles
The motion of particles is governed by Newton’s three laws of motion.
First law: A particle originally at rest, or moving in a straight line at constant velocity, will remain in this state if the resultant force acting on the particle is zero.
Second law: If the resultant force on the particle is not zero, the particle experiences an acceleration in the same direction as the resultant force. This acceleration has a magnitude proportional to the resultant force.
Third law: Mutual forces of action and reaction between two particles are equal, opposite, and collinear.
The first and third laws were used in developing the concepts of statics. Newton’s second law forms the basis of study of dynamics.
Mathematically, Newton’s second law of motion can be written:
¯F=m¯a
where ¯F is the resultant unbalanced force acting on the particle, and ¯a is the acceleration of the particle. The positive scalar m is called the mass of the particle.
2.4.1. Gravitational force
The studies and observations of planetary motions led Newton to the conclusion to the law of universal gravitation. Two particles of mass M and m attract each other with equal and opposite force along the line connecting the particles.
F=G Mm/r^2
where G: constant of gravitation.
G=66.73·10^(-12 ) 〖Nm〗^(-2) 〖kg〗^(-2)
M=5.9736·10^(24 ) kg;
r=6372.797 km
For particle of mass m on the Earth’s surface.
W=m MG/R^2 =mg
g=9.81 〖m/s〗^2
2.4.2. Impulse-momentum theorem
Linear momentum I is
¯I=m ¯v
The momentum is directly proportional to the object’s mass (m) and velocity (v). Momentum is a vector and has the same direction as velocity ( ¯v).
Newton’s second law of motion in terms of momentum:
¯F=m (∆¯I)/∆t
thus
¯F ∆t=∆¯I=m¯(v_2 )-m¯(v_1 )
is known as impulse or momentum.
The effect of a force on an object depends on how long it acts, as well as the magnitude of the force.
Example:
The system of two blocks in Fig. 2.4.1 is released from rest at t=0.
Find the acceleration of the two blocks and the cable tensile force. The pulley is massless, and the pulley bearings are frictionless.
m_1=40 kg; m_2=60 kg
2.4.3. Angular momentum of a particle
The angular momentum ¯Π is defined as the cross-product of ¯r and ¯I, and is perpendicular to the plane contain ¯r and ¯I
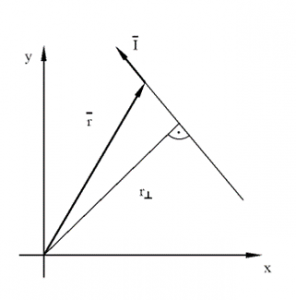
Figure 2.4.2
¯Π=¯r x¯I=¯r xm¯v
The magnitude of the angular momentum:
Π=r_⊥ mv
Relationship between net torque and angular momentum on the particle.
(d¯Π)/dt=(d( ¯r x¯I))/dt=(d ¯r)/dt x¯I+(d¯I)/dt x¯r
(d¯r)/dt x¯I=¯v xm¯v=m(¯v x¯v)=¯0
(d¯Π)/dr xr=¯0+(d¯I)/dt xr=¯F x¯r
(d¯Π)/dt=¯M
2.4.4. Work-energy methods for particles
Work is equal to displacement multiplied by the component of force along the displacement.
The component of F along s is F*cosα, the work is:
W=F*s*cosα
In general form the work:
W=¯F* ¯s
Work is scalar quantity, and units of work Nm.
Kinetic energy of an object is a measure of its ability to do work. The translational kinetic energy of an object of mass m and velocity v is:
T=1/2 mv^2
2.4.5. Collision of particles
Figure 2.4.5 shows two masses moving along the same axis in opposite direction. The masses have the constant velocities v_1 and v_2. Figure 2.4.5 shows the free-body diagram during the collision, or impact.
Figure 2.4.5
During this period of contact a compressive force acts between the two masses.
¯(F_12 )+¯(F_21 )=¯0
At the moment of the collision the two masses move together with speed u.
2.5. Kinetics of rigid bodies
The complete description of the general plane motion of rigid bodies is given by two equations
¯F=m*¯(a_c )
M_0=I_0*α
The first equation describes the translational motion of the CM, while the second describes the rotational motion about the CM.
The second equation is written in scalar form.
2.5.1. Kinetic energy of a rigid body in planar motion
Fig. 2.5.1 shows a rigid body which is in planar rotational motion about a fixed point.
Figure 2.5.1
The absolute velocity of the typical mass element dm is
v=r*ω
For the present problem, I is the mass moment of inertia of the body about the fixed point which is the instant center. Using the transfer theorem for moments of inertia, we get
I=I_0+mr_0^2
where I_0 is the mass moment of inertia of the body about the CM.
The kinetic energy term now has the form of
T=1/2 (I_0+mr_0^2 ) ω^2=1/2 I_0 ω^2+1/2 mr_0^2 ω^2
Since v_0=r_0 ω, the final form
T=1/2 mv_0^2+1/2 Iω_0^2
2.5.2. Impulse-momentum equation for rigid bodies
Newton’s second law for rotation of the body about the fixed point is:
M=I*α=I*dω/dt
Equation M=Iα integrated over a time interval with end points 1 and 2. The result is
∫_1^2▒〖Mdt= 〗 ∫_1^2▒〖Idω=I(ω_2-ω_1 ) 〗
The quantity ∫_1^2▒Mdt is the impulse of the moment M.
You can find the entire textbook of this course on this link.