Lesson 6 – General planar motion of a rigid body

2.2. General planar motion of a rigid body

The most general type of planar motion is the combination of rotation and translation. In the case of planar motion of a rigid body, all parts of the body move in parallel planes.
In the case of translational motion, every line in the body remains parallel to its original position at all time.

Fig. 2.2.2 shows the situation when the body moves with plane curvilinear motion

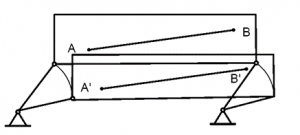
Figure 2.2.2

Any arbitrary line on the body is always parallel, in planar curvilinear paths. The velocity and acceleration at the two arbitrary A and B are
v_A=v_B
a_A=a_B

In the case of rotational motion, all particles move in circular paths about the axis of rotation. All lines in the body which are perpendicular to the axis of rotation rotate through the same angle at the same time. Circular motion of a point helps describe the rotating motion.

Figure 2.2.3

Fig. 2.2.3 shows a link of length R which rotates about fixed axis. The velocity of point A must be tangent to the path of motion. The magnitude of this velocity is given by
v=ds/dt
ds/dt=R dφ/dt=rω

2.2.1. Rotation about fixed axis

¯v=(¯r) ̇=¯ω x¯r by vector differentiation
|¯r|=constant

Figure 2.2.4

¯a=(¯v) ̇=¯ω x(¯ω x¯r)+¯α x¯r

¯(a_n )=¯ω x(¯ω x¯r)=-ω^2 ¯r

¯(a_t )=¯α x¯r

2.2.2Planar kinematics of rigid bodies

The body in Fig. 2.2.5 is initially in position by specifying the ¯(r_A ) and ¯(r_B ). ¯AB is a reference line in the rigid body.

Figure 2.2.5

At a later time, the body is in position where the reference line is ¯(A^’ B^’ ).
∆r_B=∆r_A+∆r_BA

∆r_BA=r∆φ

v_BA=lim┬(∆t→0)⁡〖(∆r_BA)/∆t〗=rω

Using ¯r to represent vector ¯(r_AB ), relative velocity may be written as the vector
¯(v_BA )=¯ω x¯r

Velocity of the B point is
¯(v_B )=¯(v_A )+¯ω x¯(r_AB )

2.2.3. Instant center of rotation

The translational velocities of the point A and B are known, it is desired to find the location of the instant center (IC) of rotation

Figure 2.2.6

Line a is perpendicular to ¯(v_A ) and line b is perpendicular to ¯(v_B ). The point of intersection of these two lines is then the instant center of rotation of the body.

Example:

The crank arm ¯OA shown in Fig. 2.2.7 rotates counterclockwise at 10 rad/sec. Find the velocity of the slider block and the angular velocity of link AB, for the position shown in the Fig 2.2.7.

¯OA=400 mm ¯AB=700 mm

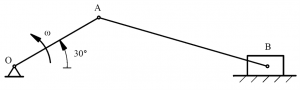
Figure 2.2.7