Lesson 5 – Kinematics of particle
2. Kinematics and kinetics
Kinematics deals with the description motion of bodies without examining the cause of the origin of the motion. The simplest moving body is a particle. A particle (point mass) defined as a body whose dimensions are negligible. If the physical element is not assumed to be particle, it is referred to as body. All bodies considered in this text are assumed to be rigid.
Two general types of particle motion may be identified. The first type is rectilinear translation, and this type of motion is straight line motion. The second general type of particle motion is called curvilinear translation.
2.1. Kinematics of particle
We know the motion if we know the location of the particle with respect to a fix reference point.
In most general case a three-dimensional coordinate system is used to define position of particle. The position vector of particle is a vector drawn from reference frame to the particle.
¯r=x¯i+y¯j+z¯k
The trajectory of a particle is a vector function of time ¯r (t), which defines the curve traced by moving particle, given by
¯r(t)=x(t)¯i+y(t)¯j+z(t)¯k
2.1.1. Velocity and speed
The particle moves distance ∆s during the time internal ∆t.
The average velocity v_avg is defined to be
v_avg=∆s/∆t
If ∆¯r is change in the position vector in the time ∆t.
2.1.3. Rectilinear motion with constant acceleration
Considering any kind of movement due to constant acceleration it is important to find the position and velocity of the object at later time.
It gives the acceleration (a), the initial position (x_0) the initial velocity (v_0)
From definition, the average acceleration
a=∆v/∆t=(v(t)-v_0)/∆t
therefore
v(t)=v_0+a∆t
From the definition average velocity, the displacement
∆s=v_avg ∆t
∆s=(v_0+v(t))/2 ∆t=v_0 ∆t+a/2 〖∆t〗^2
x=x_0+v_0 ∆t+a/2 〖∆t〗^2
The three equations are below
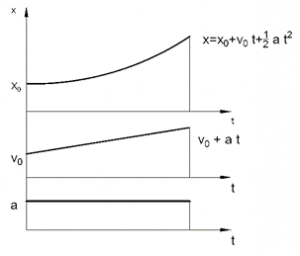
x=x_0+v_0 t+1/2 〖at〗^2
v=v_0+at
a=constant
If x_0, v_0, and and a assumed to be positive, the displacement, velocity and acceleration diagrams would have the forms shown in Fig. 2.1.6.
2.1.4.Circular motion
Uniform circular motion is a motion in a circular path with constant speed.
The angular position or angular displacement in radians
φ=s/R
The angular velocity is the rate of change of angular positions
ω=∆φ/∆t
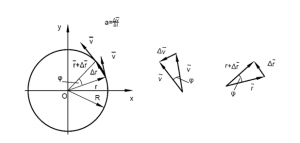
The position vector is referenced to the origin of the coordinate system.
¯r(t)=R[cos〖(ωt)¯i〗+sin〖(ωt)¯j〗 ]
The speed of a particle
v=∆s/∆t=R ∆φ/∆t=Rω
On the circular track the direction of the velocity vector is continually changing therefore:
¯a=(∆¯v)/∆t
2.1.5. Planar projectile motion in terms of component motion
Figure 2.1.10 shows the motion when a particle is launched with initial velocity in a vertical plane.
The curvilinear translational motion of the particle will be expressed now in terms of component motions in the x and y directions. In this model all air resistance effects will be neglected.
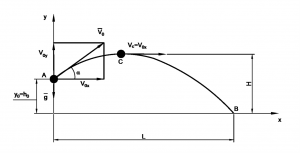
Figure 2.1.10 a particle is launched with initial velocity in a vertical plane
The motion of the particle in y direction is a case of free falling motion of body in gravitational field.
The magnitude of the acceleration a is equal to the magnitude g of the acceleration of gravitational filed.
a=-g
Equations for this case
v_y=v_0y-gt
y=y_0+v_0y t-1/2 gt^2
The gravitational acceleration in x direction is zero
Thus,
v_x=constant
Example:
Figure 2.1.10 shows a particle which is launched with initial velocity v_0=80 m/s, α=30°, h_0=100 m.
- Find the maximum height reached by the particle.
- Find the duration of the flight and the distance L at which the particle strikes the ground.
- Find the velocity with which the particle strikes on the ground.
Initial conditions are:
v_0x=v_0 cos〖α=〗 69.28 〖ms〗^(-1)
v_0y=v_0 sin〖α=〗 40 〖ms〗^(-1)
1. When the maximum height is reached
v_y=0
0=v_0y-gt
t=v_0y/g=40/9.81=4.08 s
The magnitude of the maximum height
y_max=h_0+v_0y t-1/2 gt^2=100+40·4.08-1/2·9.81·〖4.08〗^2=181.6 m
2. When the particle on strikes the ground
y=y_0+v_0y t-1/2 gt^2=100+40·t-4.905·t^2=0
t=10.16 sec
L=v_0x t=703.93
3. When the particle hits the ground t=10.16 sec
v_y=v_0y-gt=-59.67 〖ms〗^(-1)
The magnitude of the striking velocity isv=√(v_x^2+v_y^2 )=√(〖69,28〗^2+〖59,57〗^2 )=91.43 m/s