Lesson 4 – Rolling resistance, rope & belt friction

1.19. Rolling resistance

An obround object, a wheel for example, rolling on a surface without sliding is called clean rolling. This means that the contact point of the wheel is stationary relative to the surface it is rolling on.
However, the contact between the wheel and the surface is not a single point – it can not be, as it would produce infinite pressure. (See: p=F/A)

The contact surface is produced by two main factors:

• Compression of the wheel
• Indentation of the ground

The consequence of this phenomenon is that the rotating wheel has a resistive moment produced by the supporting force distributed on the contacting surface.

This resistive moment is called rolling resistance and is calculated from the supporting force and the leverage (d) between the acting lines of the resultant of the supporting (distributed) force (N) and the force loading the wheels (G).

In the boundary state of rolling:
F_N*d=M_h

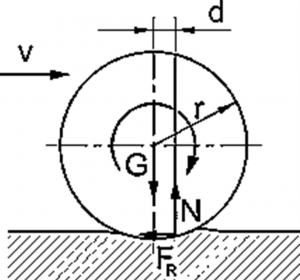
A very important requirement of clean rolling is a necessary friction between the wheel and the surface to prevent sliding.

1.20.Rope and belt friction

Winding up a rope on a bollard does not let it slip down. This phenomenon is caused by friction between the rope and the bollard.

Every rope or belt that is pushed on a cylindrical surface resists movement just like in standard cases of friction discussed earlier. The rope/belt friction depends on the contacting surfaces, the pulling forces in the rope and the central angle subtended by the rope on the surface. Please note, that this angle can be greater than 360°, in fact can be of any value.

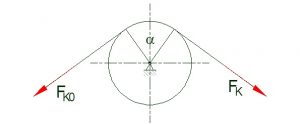
Rope friction force:
F_K=F_K0*e^(μ0*α)
Where:
μ0: the coefficient of friction between the rope and the cylinder
α: central angle of the contacting rope segment [rad].

It is demonstrated, that increasing the central angle increases the rope friction exponentially.