Lesson 1 – Introduction
Vector mechanics serves as the fundamental framework for understanding and analysing the behaviour of physical systems, ranging from the motion of celestial bodies to the mechanics of intricate machinery. It provides a powerful toolset to describe and predict the motion and equilibrium of objects, making it a cornerstone of engineering, physics, and applied mathematics.
At its core, vector mechanics deals with the study of forces and their effects on objects. Unlike scalar quantities, which possess only magnitude, vectors possess both magnitude and direction. This critical distinction allows us to precisely characterize the motion and interactions of objects in three-dimensional space.
The principles of vector mechanics find their roots in Sir Isaac Newton’s laws of motion. These laws, along with the concept of vector addition and subtraction, form the building blocks of the subject. By applying these principles, scientists and engineers can gain a deep understanding of the complex dynamics involved in various systems.
One of the fundamental concepts in vector mechanics is the concept of equilibrium. Equilibrium occurs when an object’s net force and net torque become zero, resulting in a balanced state. Understanding equilibrium is essential for designing structures, analyzing the stability of objects, and predicting the behaviour of systems at rest. The first main chapter of this book is about this concept.
Vector mechanics also plays a crucial role in studying motion and its underlying causes. By employing vector principles, we can analyse the kinematics of objects, which involves studying the geometric aspects of motion without considering the forces that cause it. The application of vector calculus techniques, such as differentiation and integration, further enables us to delve into the dynamics of systems, accounting for the forces at play. This is the topic of the second main chapter.
1 STATICS OF RIGID BODIES
1.1 ESSENTIAL BASIC TERMS AND CONCEPTS
The science of mechanics is a vast, diverse science. The most common categorization of mechanics is shown in the image below:
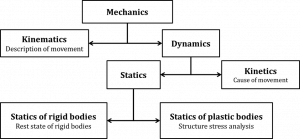
This textbook focuses on the mechanics of rigid bodies and structures. The first chapter is about statics of rigid bodies. The problems within this category are always calculated for a single moment in time, thus not taking transient effects into account.
This means that the bottom line of statics is that the inspected bodies and structures preserve their state of movement.
1.1.1 RIGID BODY
Definition: The distance of two randomly selected points of the body is constant.
This means that any force magnitude can be applied to the rigid body, it will not change its shape. This book focuses on rigid bodies, which are clearly idealized models. In reality, solid bodies and structures behave differently, but rigid body mechanics is needed to establish a foundation of knowledge for more complex, less idealized problems.
1.1.2 POINT IN MECHANICS
It can be considered as a rigid body with negligible dimensions.
1.1.1 Reference system
Right-handed cartesian coordinate system both in plane and in space.
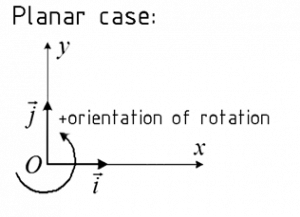
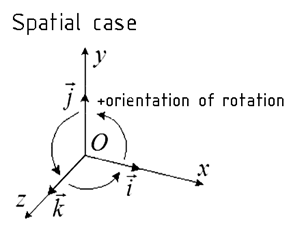
where:
𝑖 ̅- unit vector in the direction of x axis
𝑗 ̅- unit vector in the direction of y axis
𝑘 ̅- unit vector in the direction of z axis
1.1.4 THE FORCE
Definition: The mutual effect of two bodies on each other if it results in the change of movement state or deformation.
• Symbol: F, dimension: N (Newton)
• Occurs with or without contact
In case of contact, the force can be:
• Concentrated, acting at a single point
• Distributed on a line: p= G/l
• Distributed on a surface: p= F/A
Distributed forces can be substituted with a concentrated force acting in the centroid of the contact.
Eucleidan vector:
- Magnitude
- Direction
- Orientation
Vector operations are applicable.
Multiple forces can act on a body at the same time. This is called a force system. Based on Newton’s superposition principle, the forces can be decomposed or summed in the direction of two (non-parallel) lines of action in a plane common to the force.
1.2 FUNDAMENTAL THEOREMS OF STATICS
1.2.1 THEOREM 1. = NEWTON’S III. AXIOM:
The principle of action-reaction, which states that the action of two bodies on each other is always equal to each other and has the opposite orientation.
This has very important consequences:
• A force cannot exist alone, it can be exerted only if it has “something to hold onto”.
• The direction of a force only depends on which body is in the selected reference frame.
It is essential to understand this fundamental nature, to truly comprehend forces.
1.2.2 THEOREM 2. = THE REQUIREMENTS OF BALANCE
Two forces acting on a body are in balance only if the line of action of the two forces is common, their magnitude is the same and their orientation is opposite.
1.2.3 THEOREM 3. = RESULTANT FORCES
a force system with a common point of attack can always be replaced by a single, resultant force equivalent to the system. The acting point of the resulting force is the same as the acting point of the force system.
1.2.4 THEOREM 4. = SHIFTING OF FORCES
The effect of a force system acting on a rigid body does not change if we add or subtract another force system that is in balance on its own.
The consequence of the theorem is that forces acting on a rigid body can be shifted along their line of action.
1.3 MOMENT
Definition: the rotational effect of a force around a point or axis.
Simplified formula: M=F*k
1.3.1 MOMENT THEOREM
The moment of a force at a point is equal to the sum of the moments of the components of the force at the same point.
In other words, the moment of the resultant of a force system at any point in the plane is equal to the sum of the moments of the forces at the same point.
1.3.2. Resultant of parallel forces
The resultant force can be determined from: R=∑ Fi , thus the magnitude, direction and orientation are known. However, the line of action is unknown! The resultant replaces the force system, so the moment of the resultant on any point is the same as the moment of the force system. The consequence of this is the moment theorem.
1.4 BALANCE OF THREE FORCES
Conditions:
1. Their lines of action intersect at one point.
2. Their vector triangles are closed and have a continuous arrow flow.
The balance of three forces can be simplified as the balance of two forces by substituting any two of the three forces with their resultant.
1.5 BALANCE OF FOUR FORCES
Conditions:
1. Their lines of action intersect at one point.
2. Their vector polygons are closed and have a continuous arrow flow.
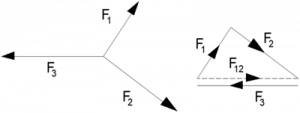
Cullmann’s drafting method: F + F1 + F2 + F3 = 0; → F + F12 + F3 = 0; F12 = S
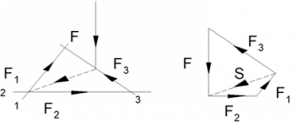
The base idea of Cullmann’s drafting method is that the resultant of two forces will always go through the intersection of the lines of action of those forces. Thus, if we search the balance of four forces, two “pairs” or sub-resultants of forces can be created of which the intersection points can be found easily. These sub-resultants are only in balance if they fulfil the requirements of balance of two forces, being in line and equal in magnitude. Thus, the resultant force must contain the two intersection points we just found. These points determine the line of action of the resultant.
1.6 REDUCTION OF FORCES
Reduction of a force is transferring the force F acting at point A to point O.
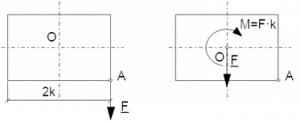
Result: the force F at point O and a moment M = F * k rotating around point O in the same direction as the original F force at point A.